Deep Learning的起源︰第二章-Neural Network的空間意義
keyword:深度學習deep learning,類神經網路Neural Network。
特徵 ${x_{1}}$代表是不是圓的,是的話=1,不是的話=-1。
特徵 ${{x}_{2}}$代表是不是硬的,是的話=1,不是的話=-1。
蘋果 又圓 又硬:
$\left[ x_{1}^{b},x_{2}^{b} \right]=\left[ -1,-1 \right]$
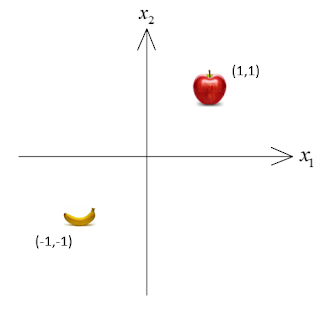
所以我們可以將上面的蘋果和香蕉畫在圖上:
接著我們假設$[{{w}_{1}},{{w}_{2}}]=[1,1]$,$b=-1$也就是:
將它繪在蘋果和香蕉的圖上就像:
聰明的你有沒有發現一件事-這條直線方程式剛好分開了蘋果和香蕉,
而L1的法向量正是$[{{w}_{1}},{{w}_{2}}]$,
${{x}_{1}}$截距是$\frac{-b}{{{w}_{1}}}$,${{x}_{2}}$截距是$\frac{-b}{{{w}_{2}}}$,
我們可以從截距的式子了解到對於線到原點的距離$b$做著調控的腳色,
假若說$b=0$那L1就會經過原點。
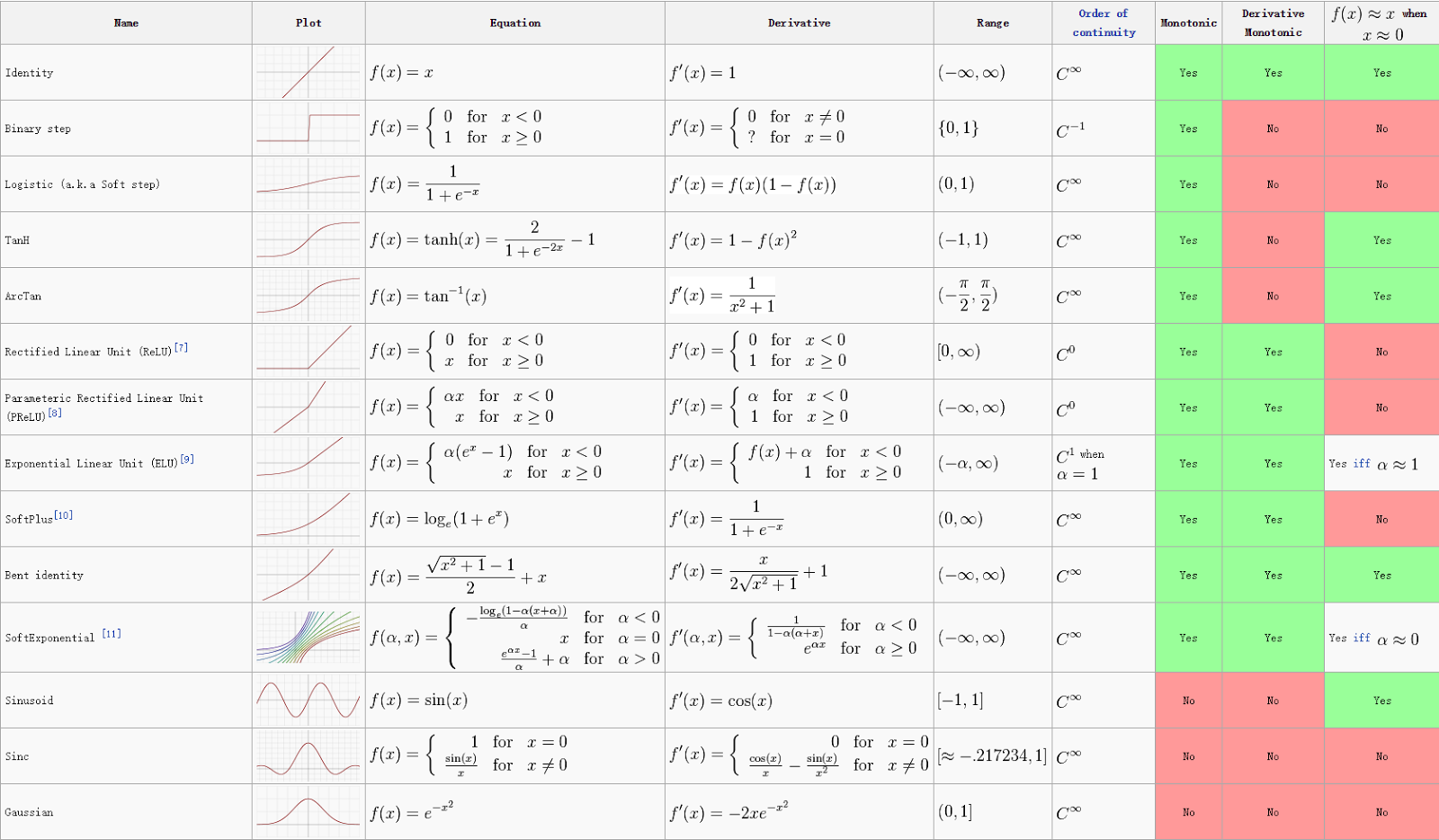
接著我們設定$f$為$\text{hardlim(binarystep)}$分別試算蘋果和香蕉的答案:
答案正是1和0,若說y=1代表蘋果,y=0代表香蕉,那我們已經成功的分類了!!!
若直接從圖來看,
我們可以知道蘋果在L1的上面所以代入後會>0,在藉由$f()$輸出1,
香蕉亦同在L1的下面所以代入後會<0,在藉由$f()$輸出0,
有沒有覺得很神奇呢?
而當輸入x有三個時ex:[x1,x2,x3],則可以把它想成一個三維問題,而神經元則是一個面,
多維就不解釋了,我想像不到XDD。
前言:
前一章我們已經將基本的類神經網路解釋完畢了,我們也了解到weight和bias的使用以及意義,然而可能有些人對數學式可能比較沒感覺(我就是QQ),所以我們這章將解釋NN(Neural Network)在空間上的意義。Neural Network的空間意義
首先我們舉一個蘋果跟香蕉的分類問題,特徵 ${x_{1}}$代表是不是圓的,是的話=1,不是的話=-1。
特徵 ${{x}_{2}}$代表是不是硬的,是的話=1,不是的話=-1。
蘋果 又圓 又硬:
$\left[ x_{1}^{a},x_{2}^{a} \right]=\left[ 1,1 \right]$
香蕉 又長 又軟:$\left[ x_{1}^{b},x_{2}^{b} \right]=\left[ -1,-1 \right]$
所以我們可以將上面的蘋果和香蕉畫在圖上:
接著我們假設$[{{w}_{1}},{{w}_{2}}]=[1,1]$,$b=-1$也就是:
${{w}_{1}}{{x}_{1}}+{{w}_{2}}{{x}_{2}}+b$
$1{{x}_{1}}+1{{x}_{2}}-1$
從上式我們可以注意到其實這就是一個直線方程式L1,將它繪在蘋果和香蕉的圖上就像:
聰明的你有沒有發現一件事-這條直線方程式剛好分開了蘋果和香蕉,
而L1的法向量正是$[{{w}_{1}},{{w}_{2}}]$,
${{x}_{1}}$截距是$\frac{-b}{{{w}_{1}}}$,${{x}_{2}}$截距是$\frac{-b}{{{w}_{2}}}$,
我們可以從截距的式子了解到對於線到原點的距離$b$做著調控的腳色,
假若說$b=0$那L1就會經過原點。
接著我們設定$f$為$\text{hardlim(binarystep)}$分別試算蘋果和香蕉的答案:
${{y}^{a}}=f\left(
1\times 1+1\times 1-1 \right)=1$
${{y}^{b}}=f\left( 1\times -1+1\times -1-1 \right)=0$
答案正是1和0,若說y=1代表蘋果,y=0代表香蕉,那我們已經成功的分類了!!!
若直接從圖來看,
我們可以知道蘋果在L1的上面所以代入後會>0,在藉由$f()$輸出1,
香蕉亦同在L1的下面所以代入後會<0,在藉由$f()$輸出0,
有沒有覺得很神奇呢?
而當輸入x有三個時ex:[x1,x2,x3],則可以把它想成一個三維問題,而神經元則是一個面,
多維就不解釋了,我想像不到XDD。
~~總整理~~
- 輸入為n個時即為一個n維的問題。
- weight表示方程式的法向量。
- bias可以解釋為方程式對圓點的距離調控值
基本上我空間概念比較好,
所以在思考DL(deep learning)想不透時都會用空間慨念去想,
在解釋時也較容易說服別人,
也請大家把這章所講的理解清楚,因為在下章我們會以空間概念解釋NN如何學習~~
歡迎有問題的人提問,即一起討論喔~~~
下一次我們將會介紹:學習x倒傳遞
謝謝大家~~


留言
張貼留言